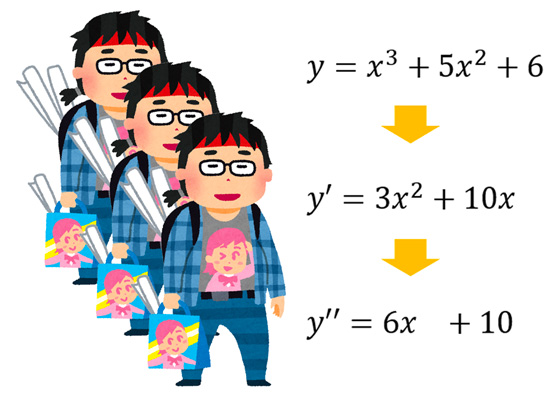アニメの中で甘酸っぱい青春を過ごしたい。コジマです。
そう、二次元の世界に行きたい。のだが、そんなときオタクはしばしば「自分を微分できれば」などという。三次元の存在である自分を微分すれば、次元がひとつ落ちて二次元になれるだろう、という発想だろう。
しかし!微分しても絵の中には入れないぞ、世のオタク達よ。
「微分自体できない」とかそういう次元の問題ではなく、できたとしても絵にはならんのだ。
高校数学では、三次関数を微分すると二次関数に、二次関数を微分すると一次関数になる、と習う。
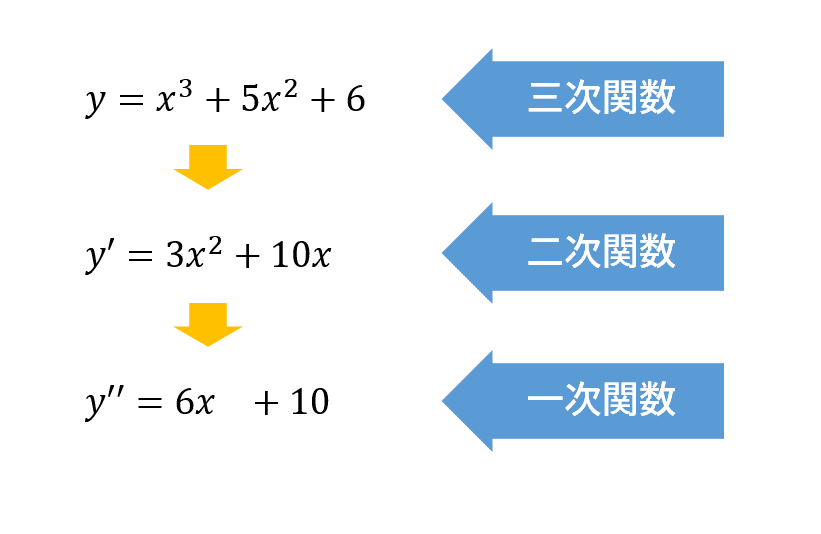
これを見ると確かに三次元が二次元になっているように思えるのだが、ここで1減っているのは「次元」ではなく「次数」であることに注意しないといけない。
文字式において、"+"や"-"で区切られた各式のことを「項」といい、(変数がxの文字式なら)xのn乗が現れる項を「次数がnの項」「n次の項」などという。微分によって減るのはこの「次数」なのだ。
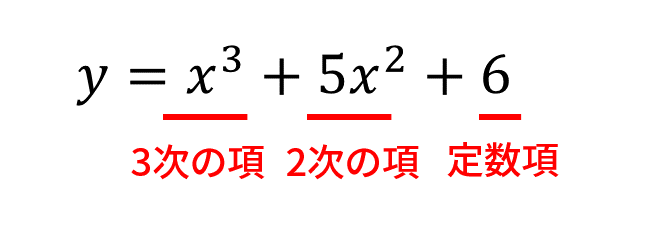
一方、次元とは「変数の種類」のこと。変数がxだけの1種類なら一次元、xとyの2種類なら二次元。
つまり、上の微分していった式は、xしか使っていないのでどれも「1次元」である。
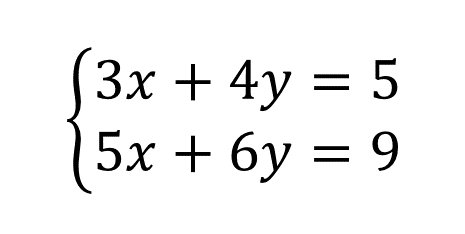 中学数学で言葉だけ出てくる「二元一次連立方程式」は、変数がxとyの二種類(=「二元」)で、次数が最大でも1(=「一次」)の「連立方程式」。
中学数学で言葉だけ出てくる「二元一次連立方程式」は、変数がxとyの二種類(=「二元」)で、次数が最大でも1(=「一次」)の「連立方程式」。「三次元」という言葉は、物体の位置や大きさを3つの変数で表せる、ということを示している。一方、絵や写真は2変数で表現できるので「二次元」。
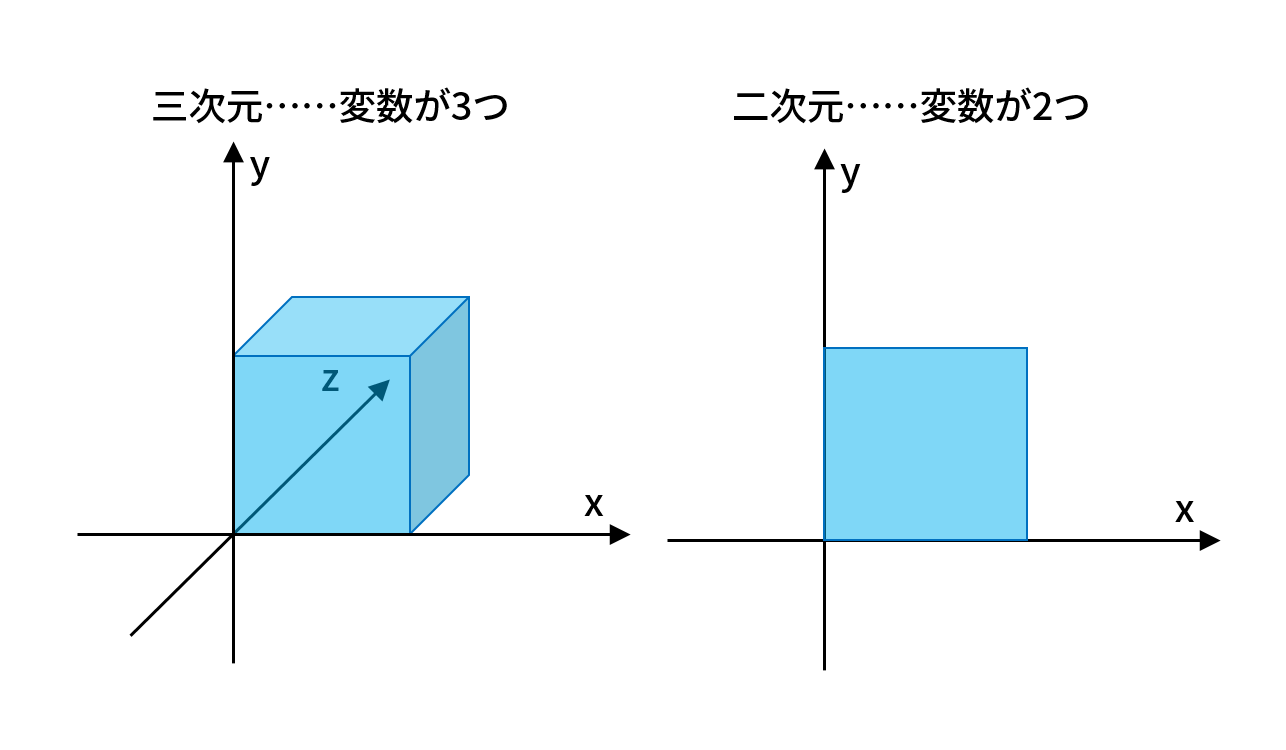
というわけで、微分は「次数を落とす手段」としては使えうるが、「次元を落とす手段」にはならないのだ。
さて、それではオタクの夢は潰えてしまったのか。いや、希望は残っている。
今やろうとしている「俗世間を捨てて絵に入ってウハウハしたい」を数学的に定義すれば、「実三次元空間を実二次元空間に移したい」(※)となる。
これを実現するものを数学では「(実三次元空間から実二次元空間への)写像」という。※現実空間における物体の座標は3つの実数で表せるから、これは独立な3つの実数体の直積=実三次元空間である、と考える。平面空間も同様。
 立ててる指が違うのはご愛嬌
立ててる指が違うのはご愛嬌「写像」という言葉は高校数学まででは出てこないが、基本的には「関数」と同じような意味で、別の2つの集合(今回の例なら三次元空間と二次元空間)を結びつけるものである。
ここでは「モノAをモノBに変更する処理」程度に考えてもらって良い。Aが生の牛肉、Bがステーキだとしたら、「焼く」という行為が写像である。(なので、微分することも写像のひとつではある。)
関数y=f(x)でxの値を決めるとyの値が出てくるのと同様に、現実空間の座標を平面座標に対応させる写像があれば、現実を絵にすることができる。一番簡単な写像は、「三次元上の物体からある平面(スクリーンに当たる)に向けて垂直に各点を移すもの」として定義できる(数学的には「射影」)。これはスクリーンから物体を見たときに見える映像そのものであり、要するに「写真」にあたる。
ただし、オタクをカメラで映してもそれはただのオタクの写真なので、夢からは程遠い。何かが足りない。
夢見る二次元の世界は、絵特有の色使いがなされているはずだ。すなわち、空間の座標だけでなく、色も変換対象に加える必要がある。数学的に言えば「実三次元空間×色空間から実二次元空間×色空間への写像」。
 三原色を表す変数の定義域をいずれも0~255と定めれば、色空間は実数体の部分集合[0, 255]3つの直積
三原色を表す変数の定義域をいずれも0~255と定めれば、色空間は実数体の部分集合[0, 255]3つの直積しかも、現実空間とアニメ絵ではしばしば物体の造形(顔のパーツの配置など)が異なるから、ただの射影ではうまくいかない。
物体を絵として違和感がないように平面上に配置し、適切な色を設定する一連の操作がここでいう「写像」であり、普段これをやってくれているのが画家やイラストレーターということになる。
とりあえず、微分では二次元には行けないよ(使うなら写像だね)ということである。
……が、重大な問題点が残っている。写像では「絵に物体を写す」ことしかできないので、仮に絵の中に意識を持って動ける自分を写し出したとしても、自分本体は現実空間に残ったまま。何も解決しないじゃないか!
それから、「夢の二次元世界」の多くは現実空間を変換したものではなく「クリエイターの想像の中にある空間」を絵に落とし込んだものなので、現実がダメなら絵にしてもダメ。
……自分で書いていて悲しくなってしまった。おしまい。