どうも~コジマです。
今回のテーマは「量子コンピュータ」。
「『りょうこ』って誰?」レベルの人に説明すると、量子(りょうし)とは「物理量の最小単位」のことで、そのくらいのミクロな世界を扱う学問を「量子力学」という。
それに「コンピュータ」がついている。何か知らんけどSFっぽいぞ。
何か知らんじゃいかんので辞書を引いてみる。
物質の量子力学的な性質を利用して動作するコンピューター。複数の計算を同時に実行でき、スーパー-コンピューターの数億倍ともいわれる高速計算が可能とされる。
どうやら計算が速いらしい。でも、「量子力学的な性質を利用して」?やっぱりいまいち分からない。
そこでこの動画をご覧いただきたい。量子コンピュータについてわかりやすく解説してくれる(英語だけど日本語字幕とイラストがあるので大丈夫)。
(これはドイツのグループが公開している"In a Nutchell"(=「要するに」)シリーズのひとつ。他の動画もいろいろな事柄の「要するに」を解説してくれている)
わかりやすいのは確かなのだが、それでも難しい。量子力学難しい。
そこで今から、この動画に基いてよくわからないポイントを解説しようと思う。
目次
トランジスタ

私たちが普段使っているコンピュータは、イラストのような「トランジスタ」を組み合わせて情報を処理する。
トランジスタは動画の通り、スイッチ(イラストの左側にある部分)に加わる電圧の値に応じて、回路(イラストでいう上から下につながった部分)をつないだり切ったりする。
これを組み合わせて複雑な処理を行えるようにしたのが集積回路(IC)である。
トランジスタの大きさは動画が作られた当時14ナノメートル、現在では10ナノメートルくらいまでは小さくなっているが、これ以上の小型化は、粒子が壁を通り抜ける(トンネル効果)など、通常の物理法則が通用しない領域に入ってしまうため、難しいとされる。
7ナノメートル、5ナノメートルくらいまでは研究がなされているようだが、コンピュータをこれ以上高性能化させるためには小型化以外の方法を追求しなければならなくなっている。

重ね合わせ

動画に出てきたキーワード「重ね合わせ」。量子コンピュータ、ひいては量子力学を考える上で重要な概念なので説明しておく。
先ほど述べた「通常の物理法則が通用しない」ミクロの世界では、物理量は測定するまで曖昧であり、測定した瞬間にいずれかの値に決まる(収束する)。
これは「ひとつの物体の状態が複数同時に存在している」と表現できる。これを重ね合わせと呼んでいるのだ。
 上の絵の0と1が混じった状態が、スポットライトを当てた(観測した)瞬間に0か1に決まる。重ね合わせが肝だ
上の絵の0と1が混じった状態が、スポットライトを当てた(観測した)瞬間に0か1に決まる。重ね合わせが肝だなるほどわからん。とりあえず、このようなミクロの世界を研究する量子力学では、重ね合わせを前提として物事を考えるということを頭に入れて以下を読んでほしい。
量子ビット
今までのコンピュータでは情報を0と1(ビット)で表していた。これに対し、量子コンピュータでは量子ビット(qubit)を用いる。
量子ビットは、ミクロな物質量について、それが「0である確率」と「1である確率」をセットで表したもの。
量子ビットの状態は、しばしば下図のような球(ブロッホ球という)の上の点で表される。地球儀のようなもので、北極が|0〉(必ず0に収束するビット)、南極が|1〉(必ず1に収束するビット)を表し、緯度が大きいほど0または1に収束しやすい。
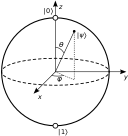
By Smite-Meister (Own work) [CC BY-SA 3.0 or GFDL], via Wikimedia Commons
量子ビットは、測定した瞬間に0と1が決定する。逆に言えば、測定しないまま扱えば0と1の両方を同時に表すことができる。
量子コンピュータでは、このような量子ビットを、その出現確率を動かしていくことで計算を行う。上のブロッホ球でいえば、これを転がしたり反転したりを繰り返していくとみなせるだろうか。
そうした操作を行って出力された量子ビットは、期待される値(0か1)が出やすいような確率を持つ。これを測定すれば計算結果が得られるというわけだ。
今は1つの量子ビットしか考えていないが、これをいくつも並べ、複数の量子ビットに対して操作を行えば、既存のコンピュータと同じ計算を高速に行える量子コンピュータができ上がる。
量子もつれ
動画に出てきたので一応説明すると、「2つの粒子が遠く離れていても、片方を観測すると(その粒子だけでなく)もう片方も値が定まる」現象のことを量子もつれという。何を言っているんだ。
とりあえず、この記事では理解しなくてもやっていけるので分からなくてもよい。
量子コンピュータでできること
量子コンピュータ、冒頭でも説明したが、計算がめちゃくちゃ速くなる。
動画で出てきたデータベース検索。

「いくつかのものから欲しいものを探し出す」という単純な操作だが、これが速くなる。
例えば、4桁のダイヤル式の鍵があり、その番号を忘れてしまったとする。片っ端から試すしかない……。
「0000」から当たっていき、もし暗証番号が「0003」なら4回試せば済むし、「5000」なら5001回めで開くが、最悪「9999」なら10000回試すことになる。
このように、普通に考えれば、N個のものから1個目的のものを取り出すには平均N/2回試さなければならないが、量子コンピュータを使うと√N回くらいの操作で見つけることができるという。
……地味?確かに地味だが、Nが大きいと差が大きくなる(Nが100倍になったとき、N/2は100倍になるが√Nは10倍で済む)し、シンプルな分使う機会がとても多いので、これだけで計算のスピードがグッと速くなる。
そして、タイトルにもある問題のセキュリティ。
通信で広く利用されているRSA暗号は、素因数分解(35→5×7のように整数を素数の積に変換する問題)が難しいことを利用して、暗号化の鍵に2つの大きな素数の積を用いた暗号だ。
1000ビット(10進数で300桁)以上の整数の素因数分解は現在のコンピュータではいくら待っても解き終わらないので、鍵はバレないし安全だとされている。
しかし安全なのはコンピュータで解けない限りの話。量子コンピュータを用いて素因数分解を短時間で解く方法が既に考案されており、実際に数ビットの量子コンピュータで実証されている。
もし量子コンピュータが実用化された暁には、RSA暗号の信頼性が失われ、使えなくなってしまう。優秀な暗号アルゴリズムであるだけに混乱は避けられそうにない。
まとめ
量子コンピュータは、まだ数ビットレベルの実験段階であるが、今後扱える量子ビットの数が増えれば、今のコンピュータでできないことができるようになるだろう(もちろん暗号が使えなくなるなどの困ることもある)。
動画の最後は「技術に限界はあるのか?やってみなければわからない」と締めくくられている。「トランジスタの小型化」に限界が訪れ「量子コンピュータ」が生まれたように、量子コンピュータのその先には想像もしない未知の技術があるのかもしれない。
それでは復習にクイズをどうぞ。