こんにちは、藤原です。
最近、新型コロナウイルスについての報道を耳にしない日はありません。その中で、軸がだんだん詰まっていく、何だか気になるグラフを目にしたことはありませんか? 片対数グラフと呼ばれるそのグラフ、どういう仕組みなのか、どう役に立つのかを今こそ知っておきましょう。
指数・対数
片対数、つまり対数を知るためには、まず指数を知らなければなりません。「2×2×2=8」という式を、指数と対数、両方の表現の仕方で見てみましょう。
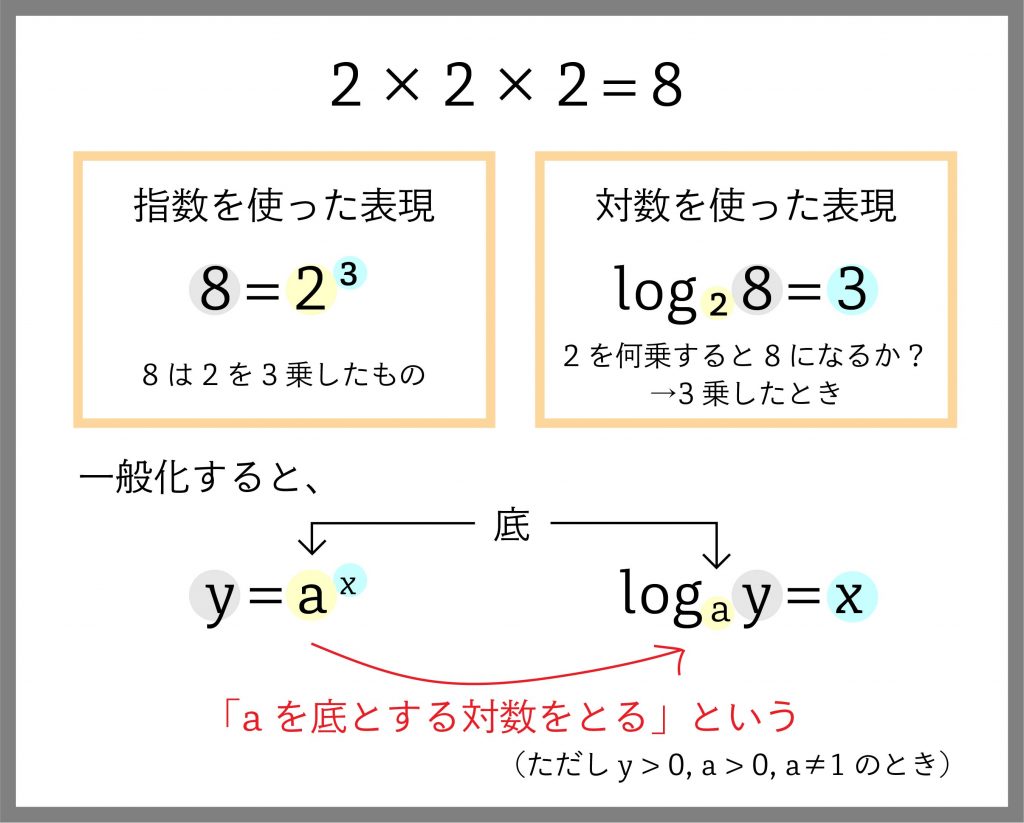
つまり、ax=yとlogay=xは本質的に同じだということが何となくわかりました。
ところで、2つの数字xとyの間に「底aをx回かけたらyになる」という関係が一貫してあるとき、「yはxの指数関数である」といいます。本質的に同じである対数を使うことで、指数関数はより扱いやすくなります。
底aをグラフから知るにはどうしたらいい?
ここで、「xとyはわかるのに、底aがわからない。」という状況を考えてみましょう。指数関数のようになっていそうだけど、肝心の底がわからないという状況です。
とりあえず10を底とする対数(常用対数)をとります。詳しい説明は省きますが、左辺はy→log10y、右辺はax→log10ax=xlog10aとなります。
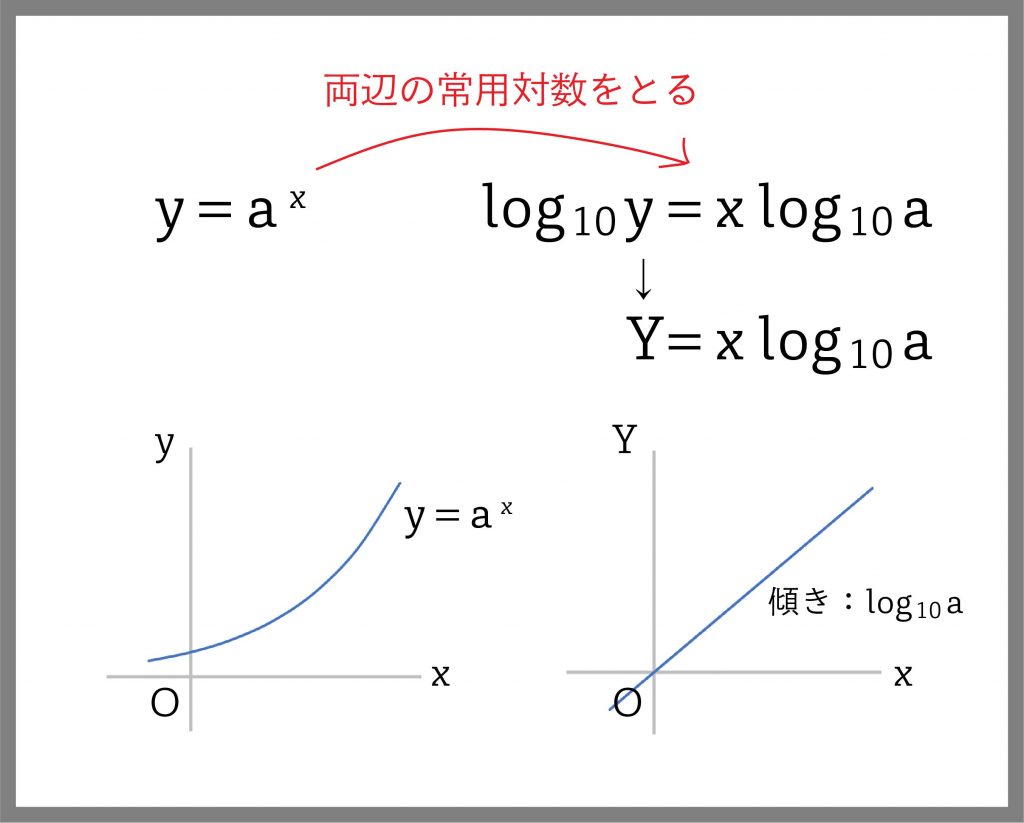
log10yを新しい変数Yと見れば、Y=xlog10aは一次関数であり、グラフは直線になります。直線の傾きであるlog10aはグラフから簡単に見てとれます。log10aがわかればaは求められるので、グラフからaが求められるようになりました。
具体例として、2020年3月における東京都の新型コロナウイルス累計患者数を分析し、底aを調べてみましょう。底aは、「1日あたりに感染者が何倍になるか」を表します。データの始まりである2020/3/1をx=0としました。
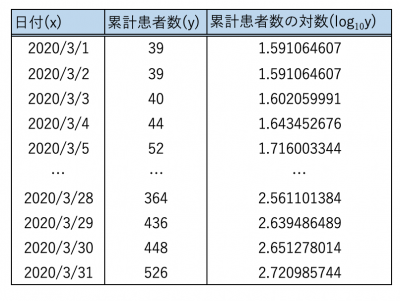
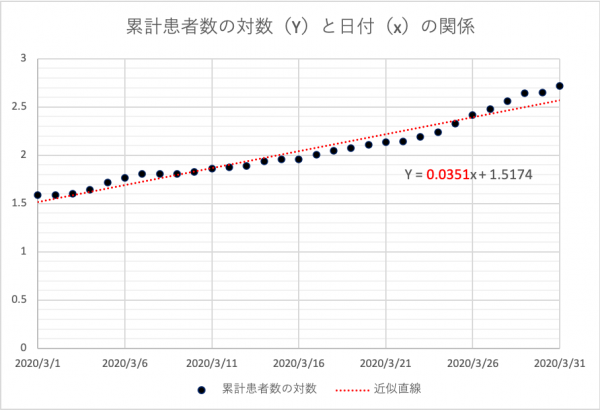 累計感染者数の対数を計算し、xとYのグラフとしてプロット(※)した
累計感染者数の対数を計算し、xとYのグラフとしてプロット(※)したlog10a≒0.0351なので、a≒100.0351、おおよそ1.08だと計算できます。2≒1.089なので、「感染者数は大体9日で倍増」していることもわかります。
※統計などで、データを図表上に示すこと。
片対数グラフ
しかし、log10y(=Y)をいちいち計算するのは非常に面倒です。「log10yを新しい変数Yと見れば、」という操作をグラフ上でやってしまえたら便利ですよね。これを可能にするのが片対数グラフです。
 片対数グラフの目盛り
片対数グラフの目盛りyの値を対数軸の目盛りにしたがってプロットすると、log10yを計算して普通の方眼紙にプロットしたときと同じグラフが書けます。
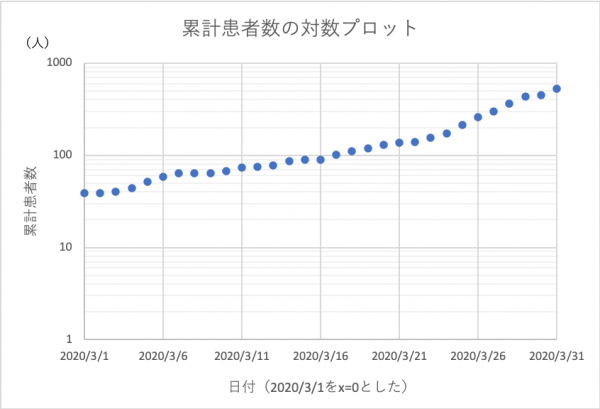 片対数グラフを用いてyを直接プロットした。上のグラフと同じ形になっていることがわかる。
片対数グラフを用いてyを直接プロットした。上のグラフと同じ形になっていることがわかる。最近話題の、新型コロナウイルス感染者数の推移を表すグラフは、片対数グラフの実用例として最たるものです。ここまで読んだ方なら、片対数グラフから、底(この場合は感染者数の増加率と呼べる)の変化なども見てとることができるでしょう。